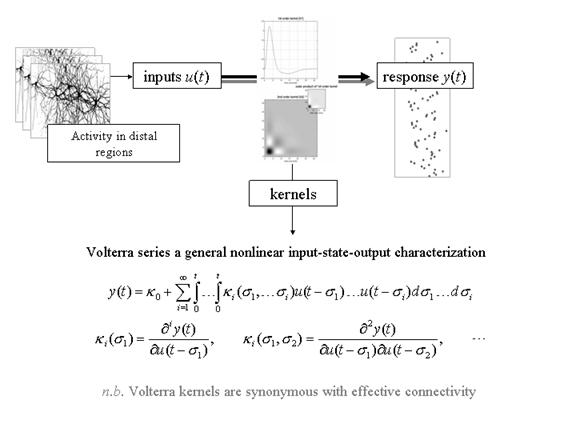
Figure 14
Schematic depicting the causal relationship between the outputs and
the recent history of the inputs to a nonlinear dynamical system, in this
instance a brain region or voxel.
This relationship can be expressed as a Volterra series, which expresses
the response or output y(t) as a nonlinear convolution of the
inputs u(t), critically without reference to any [hidden] state
variables. This series is simply a
functional ![]() is
the ith order kernel. Volterra series have been described as a
'power series with memory' and are generally thought of as a high-order or
'nonlinear convolution' of the inputs to provide an output. Volterra kernels are useful in characterizing
the effective connectivity or influences that one neuronal system exerts over
another because they represent the causal characteristics of the system in
question. Neurobiologically they have a
simple and compelling interpretation
they are synonymous with effective connectivity. It is evident that the first-order kernel
embodies the response evoked by a change in input at
is
the ith order kernel. Volterra series have been described as a
'power series with memory' and are generally thought of as a high-order or
'nonlinear convolution' of the inputs to provide an output. Volterra kernels are useful in characterizing
the effective connectivity or influences that one neuronal system exerts over
another because they represent the causal characteristics of the system in
question. Neurobiologically they have a
simple and compelling interpretation
they are synonymous with effective connectivity. It is evident that the first-order kernel
embodies the response evoked by a change in input at ![]() . In other words it is
a time-dependant measure of driving
efficacy. Similarly the second order
kernel reflects the modulatory
influence of the input at
. In other words it is
a time-dependant measure of driving
efficacy. Similarly the second order
kernel reflects the modulatory
influence of the input at ![]() on the evoked response
at
on the evoked response
at ![]() . And so on for higher
orders.
. And so on for higher
orders.