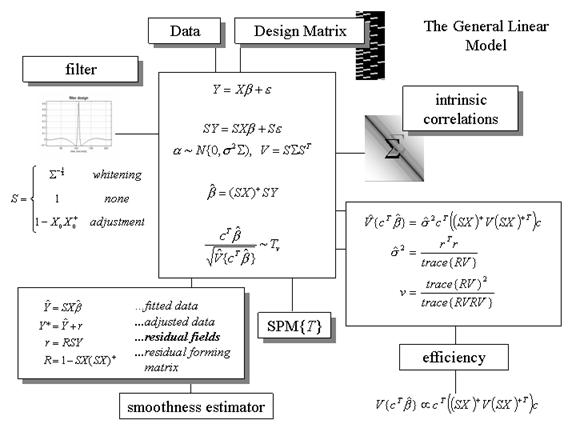
Figure 4
The
general linear model. The general linear
model is an equation expressing the response variable Y in terms of a linear combination of explanatory variables in a
design matrix X and an error term
with assumed or known autocorrelation S. In fMRI the data can be filtered with a
convolution or residual forming matrix (or a combination) S, leading to a generalized linear model that includes [intrinsic]
serial correlations and applied [extrinsic] filtering[1]. Different choices of S correspond to different estimation schemes as indicated on the
upper left. The parameter estimates
obtain in a least squares sense using the pseudoinverse (denoted by +) of the
filtered design matrix. Generally an
effect of interest is specified by a vector of contrast weights c that give a weighted sum or compound
of parameter estimates
referred to as a contrast. The T statistic is simply this contrast
divided by its the estimated standard error (i.e. square root of its estimated variance). The ensuing T statistic is distributed with 
v degrees of
freedom. The equations for estimating
the variance of the contrast and the degrees of freedom associated with the
error variance are provided in the right-hand panel. Efficiency is simply the inverse of the
variance of the contrast. These expressions are useful when assessing the
relative efficiency of experimental designs.
The parameter estimates can either be examined directly or used to
compute the fitted responses (see lower left panel). Adjusted data refers to data from which
estimated confounds have been removed.
The residuals r obtain from
applying the residual-forming matrix R
to the data. These residual fields are
used to estimate the smoothness of the component fields of the SPM used in
random field theory (see Figure 7.htm).
