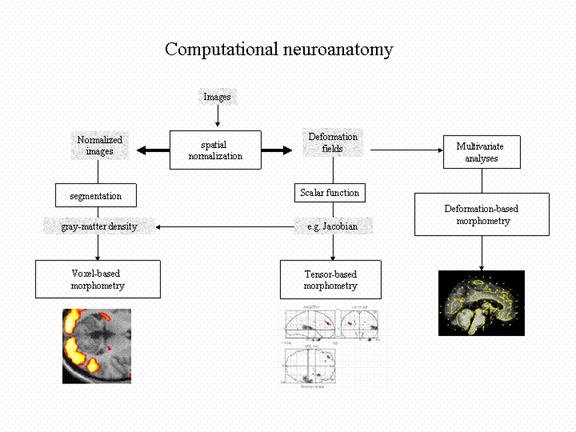
Figure 3
Schematic illustrating different procedures in computational anatomy. After spatial normalization, one has access to the normalized image and the deformation field implementing the normalization. The deformation or tensor field can be analyzed directly (deformation-based morphometry) or can be used to derive maps of formal attributes (e.g. compression, dilatation, shear etc.). These maps can then be subject to conventional voxel-based analyses (tensor-based morphometry). Alternatively the normalized images can be processed (e.g. segmented) to reveal some interesting aspect of anatomy (e.g. the tissue composition) and analyzed in a similar way (voxel-based morphometry). Techniques developed for tensor-based morphometry can be absorbed into voxel-based morphometry to prove a unified framework. For example, before statistical analysis Jacobian, or voxel-compression, maps can be multiplied by gray-matter density maps. This endows volumetric changes, derived from the tensor, with tissue specificity, based on the segmentation.