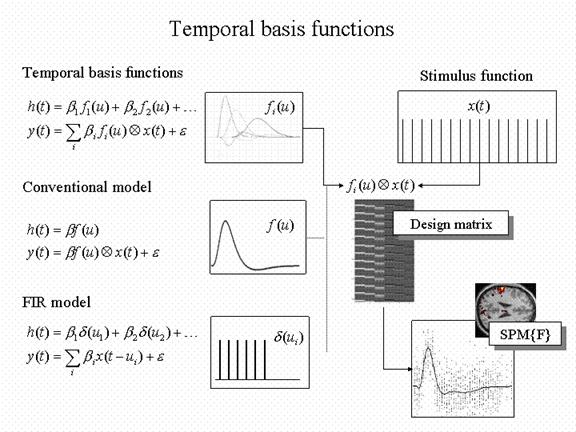
Figure 6

Temporal basis functions offer useful constraints on the form of the estimated response that retain (i) the flexibility of FIR models and (ii) the efficiency of single regressor models. The specification of these constrained FIR models involves setting up stimulus functions x(t) that model expected neuronal changes [e.g. boxcars of epoch-related responses or spikes (delta functions) at the onset of specific events or trials]. These stimulus functions are then convolved with a set of basis functions of peri-stimulus time u, that model the HRF, in some linear combination. The ensuing regressors are assembled into the design matrix. The basis functions can be as simple as a single canonical HRF (middle), through to a series of delayed delta functions (bottom). The latter case corresponds to a FIR model and the coefficients constitute estimates of the impulse response function at a finite number of discrete sampling times. Selective averaging in event-related fMRI (Dale and Buckner 1997) is mathematically equivalent to this limiting case.