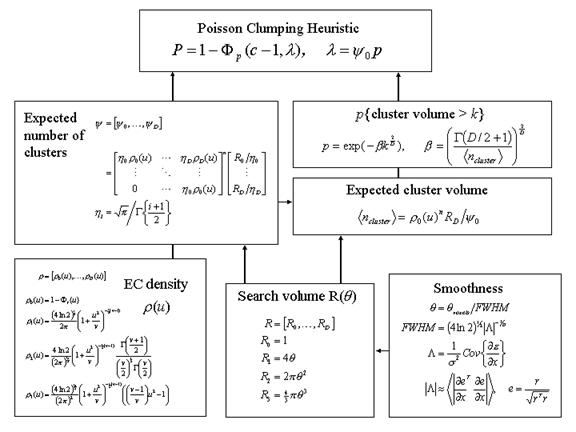
Figure 7
Schematic
illustrating the use of Random Field theory in making inferences about
SPMs. If one knew where to look exactly,
then inference can be based on the value of the statistic at a specified
location in the SPM, without correction.
However, if one did not have an anatomical constraint a priori, then an adjustment for
multiple dependent comparisons has to be made.
These corrections are usually made using distributional approximations
from GRF theory. This schematic deals
with a general case of n SPM![]() degrees of freedom v)
and the resel counts. The EC density is
the expected EC per unit of D-dimensional
volume of the SPM where the D
dimensional volume of the search space is given by the corresponding element in
the vector of resel counts. Resel counts
can be thought of as a volume metric that has been normalized by the smoothness
of the SPMs component fields expressed in terms of the full width at half
maximum (FWHM). This is estimated from the determinant of the
variance-covariance matrix of the first spatial derivatives of e, the normalized residual fields r (from Figure
4.htm). In this example equations
for a sphere of radius q
are given. F denotes the cumulative
density function for the sub-scripted statistic in question.
degrees of freedom v)
and the resel counts. The EC density is
the expected EC per unit of D-dimensional
volume of the SPM where the D
dimensional volume of the search space is given by the corresponding element in
the vector of resel counts. Resel counts
can be thought of as a volume metric that has been normalized by the smoothness
of the SPMs component fields expressed in terms of the full width at half
maximum (FWHM). This is estimated from the determinant of the
variance-covariance matrix of the first spatial derivatives of e, the normalized residual fields r (from Figure
4.htm). In this example equations
for a sphere of radius q
are given. F denotes the cumulative
density function for the sub-scripted statistic in question.