Long-term forecasting of the COVID-19 epidemic
Dynamic Causal Modelling, UCL, UK
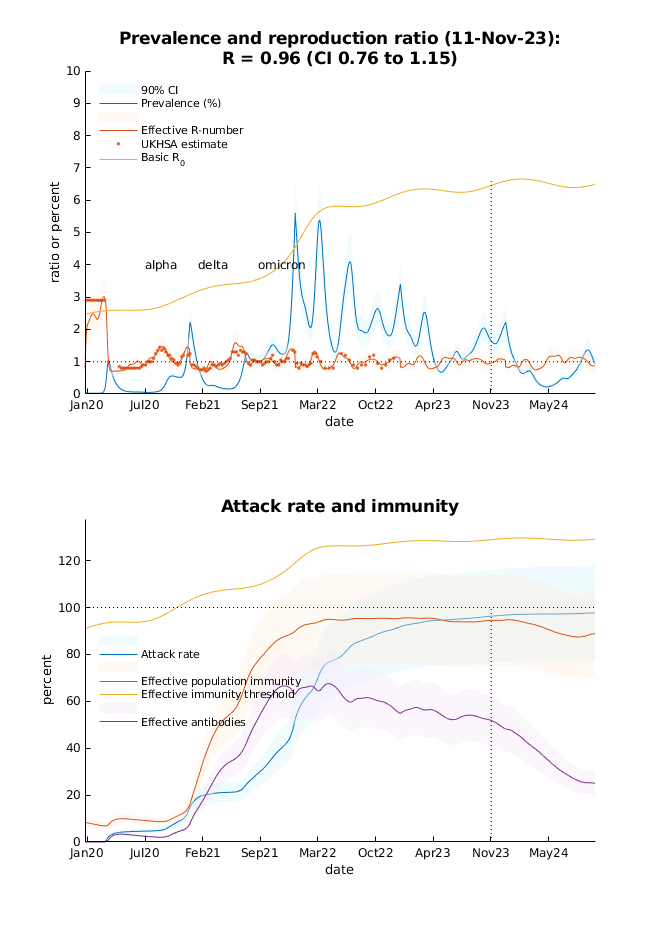
- As predicted, hospital admissions peaked in early (6th) of October. The next small peak in prevalence—of about 2%—is anticipated in early (1st) January 2024. The effective population immunity should remain at 95% for the forthcoming months. This speaks to an endemic equilibrium with seasonal fluctuations in prevalence—between 0.3% and 1.3%—over the forthcoming year.
- The real-time estimate of the R-number is 0.96 (credible interval from 0.76 to 1.15) on 11 Nov 2023.
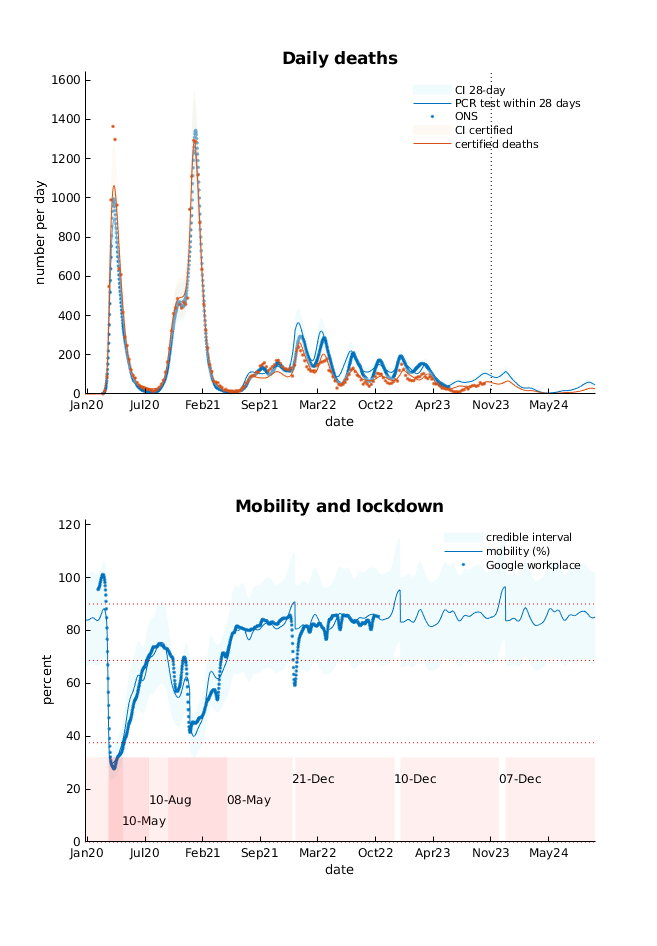
- The 7-day average of (certified) deaths in the UK may rise to about 50 over autumn, peaking in mid-January 2024.
- These predictions include prevalence–dependent behavioural changes: contact rates should continue to fluctuate between 84% and 96% of pre-pandemic rates, for the foreseeable future.
- The basic reproduction number R0 is estimated to be 6.4. This reflects an 43% increase in transmission risk, relative to the average since 1 Jan 2020. This estimate includes viral mutation and seasonality effects.
- Current estimates of the vaccination efficacy are:
- preventing infection: 29.1% (CI 26.7 to 31.6)
- preventing transmission following infection 51.4% (CI 49.3 to 53.3)
- preventing serious illness when symptomatic (age 15-34) 73.0% (CI 72.3 to 73.7)
- preventing serious illness when symptomatic (age 35-70) 61.7% (CI 60.7 to 62.7)
- preventing fatality when seriously ill 82.7% (CI 81.7 to 83.6)
- The corresponding cumulative (vaccinated vs. unvaccinated) risks are:
- relative risk of infection 70.9%
- relative risk of mild illness 48.6%
- relative risk of severe illness 16.8%
- relative risk of fatality 2.9%
- The average serial interval is 4.1 days
- The average period between exposure and becoming infectious is 2.4 days
- The average asymptomatic period is currently 2.0 days
- (Symptomatic) IFR: likelihood of dying from COVID-19 (%)
For reference, the probability of dying from flu is aboutAge group 0-14 15-34 35-69 70+ recent vaccination: 0.000 0.000 0.000 0.005 no vaccine protection: 0.000 0.000 0.003 0.062 Age group 5-17 18-49 50-64 65+ 0.000 0.002 0.009 0.022
These headlines furnish a national picture of the epidemic and obscure regional variations. Please see the national dashboard for the data fits upon which these forecasts are based and accompanying confidence intervals.
These long-term forecasts are based upon a dynamic causal model (DCM) of viral transmission and mitigated responses. This particular (age-stratified) model is equipped with a vaccination state that affords immunity of various kinds (i.e., reduces the risk of infection, transmission, developing serious illness and dying when seriously ill).
The DCM generates various data that quantify the progression of the epidemic, including the number of reported (first) vaccinations. These data are used to estimate model parameters controlling contact rates, transmission risk and periods of infectiousness using standard variational procedures. Crucially, these variables are themselves time-dependent and depend upon mitigating responses, modelled as the (prevalence-dependent) probability of moving from low to high contact rate locations (e.g., from home to the workplace). The data include daily positive tests, reported deaths within 28 days of a positive PCR test, certified deaths disaggregated by age and place of death, hospital admissions, contact rate proxies, such as car use and Google mobility data, and so on.
Much like weather forecasts, the ensuing predictions should not be overinterpreted because there is an inherent (although quantified) uncertainty about underlying epidemiological and sociobehavioural variables. These reports are released on a monthly basis so that people can see how the predictions change — and uncertainty resolves — as time progresses and more data are assimilated.
Because the DCM combines an epidemiological model with an agent-based behavioural (and testing) model, it can predict mitigating responses to changes in community transmission. These predictions are the most likely outcomes given population responses to date. In other words, DCM does not rely on information about future scenarios (e.g., roadmaps for unlocking). This complements (e.g., SPI-M projections of reasonable worst-case scenarios that assume a particular schedule of interventions and epidemiological parameters. Generally, the most likely predictions of mitigated responses—i.e., what is likely to happen—are more optimistic than worst-case projections of unmitigated responses—i.e., what could happen.
Summary graphs
In the summary graphs below, the lines and shaded intervals correspond to predictions and 90% credible intervals, while the dots are (smoothed) data upon which the estimates are based. Some of these data have been deprecated; however, all available data are used to inform model parameter estimates.
Prevalence and reproduction ratio: this panel provides a forecast of (i) the prevalence of infection and (ii) the reproduction ratio or R-number (blue and orange lines, respectively) with their accompanying confidence intervals (shaded areas). These forecasts are based upon parameters estimated from data up until the reporting date (the vertical line). The data include GOV.UK estimates of the R-number, which are shown for comparison with the DCM estimates. The basic reproduction ratio (R0 – yellow line) can be read as the R-number in the absence of any mitigating reductions in contact rates. This reflects fluctuations in transmission risk due to seasonality effects and viral mutations. The ‘alpha’, ‘delta’ and ‘omicron’ indicate when the corresponding variants were introduced to the UK. The current DCM does not model the multiple strains or variants separately: it assumes viral spread can be approximated with a mixture, whose epidemiological parameters (e.g., transmission risk) change smoothly over time.
The DCM estimate of the effective R-number is based upon a generative model (i.e., a real-time estimate using data assimilation). The corresponding consensus estimates from the UKHSA are based upon retrospective (e.g., Bayesian regression) analysis of recent data and are therefore treated as a lagged estimator. The orange dots correspond to the UKHSA estimates moved backwards in time by 16 days from their date of reporting.
Attack rate and immunity: this panel shows long-term forecasts of attack rate, population or herd immunity and the percentage of people who have seroconverted following vaccination (in blue, red and purple, respectively). In addition, an estimate of the effective immunity threshold is provided under simplifying (SIR) assumptions (yellow line).
The attack rate corresponds to the number of people who have been infected since the onset of the outbreak (blue line). This can be supplemented with a small proportion of the population that have pre-existing immunity (e.g., mucosal immunity or cross immunoreactivity with other SARS viruses). The combination underwrites herd or population immunity, read here as the proportion of people with seropositive or seronegative (e.g., T cell) immunity.
The effective immunity threshold is based upon the effective reproduction ratio under pre-pandemic contact rates, adjusted for vaccine efficacy. The reproduction ratio corresponds to the product of the contact rate, transmission risk and mean infectious period. Note that the effective immunity threshold fluctuates. This reflects the fact that transmission risk changes with time. In this model, transmission risk is modelled as a seasonal fluctuation multiplied by a smooth (increasing) function of time. A fluctuating transmission risk accommodates changes in transmissibility (e.g., due to viral evolution) that is contextualised by seasonal variations in transmission (e.g., due to changes in temperature, humidity, socialising outdoors and the propensity for aerosol transmission).
Based upon the changes in testing, death rate and other data, one can estimate the efficacy of vaccination at several points in the chain from infection to death. This DCM is equipped with two infection states: infected (i.e., exposed) versus infectious (i.e., contagious) and two clinical states: mildly symptomatic versus systemic illness. The efficacy of vaccination is modelled in terms of the relative risk of (i) becoming infected, (ii) becoming infectious after exposure to the virus (i.e., being able to transmit the virus), (iii) becoming seriously ill when mildly symptomatic, and (iv) dying when seriously ill. The relative risk of becoming infected subsumes contact rates and transmission risk. These relative risks can be expressed in terms of conditional efficacies or composed to evaluate the cumulative risk of morbidity and mortality, relative to not being vaccinated. Note that parameterising vaccine efficacy in this way means that a loss of protection is modelled by moving—with a small probability—to a non-vaccinated state (c.f., waning immunity).
Daily deaths: this panel shows fatality rates as assessed by patients who died within 28 days of positive PCR test and people who died from certified COVID-19. The former represents an underestimate of COVID-related mortality, where the degree of underestimation depends upon testing rates. The discrepancy is modelled by evaluating the probability of succumbing to COVID-19 and having had a positive PCR test within 28 days.
Mobility and lockdown: a long-term forecast of mitigating (i.e., protective) sociobehavioural responses, based upon car use as quantified by the Department of Transport and—in this graph—Google workplace and retail activity. These measures of mobility are expressed in terms of the percentage of pre-pandemic levels. The expected mobility has been thresholded at three levels to illustrate different levels of lockdown. The dates on the lower (graded pink) bar annotate a transition from a more protective level of mobility to a less protective level. Forecasts of mobility are based upon underlying contact rates that depend upon the prevalence of infection, which are then modulated with a smooth function of time.
This dynamic causal model includes age-stratification into four groups (below the age of 15, between 15 and 35, between 35 and 70, and over 70 years of age). The contact rates within and between the groups (for high and low contact rate locations) are estimated from the data, under mildly informative lognormal shrinkage priors. Please see the following technical report for further technical details.
Changes since last report:
- Slow increases in T-cell immunity (Tnn) modelled with a logarithmic function of time (as opposed to a linear function)
Software note: The figures in this report can be reproduced using annotated (MATLAB) code available as part of the free and open source academic software SPM (https://www.fil.ion.ucl.ac.uk/spm/), released under the terms of the GNU General Public License version 2 or later. The routines are called by a demonstration script that can be invoked by typing >> DEM_COVID_UK4 at the MATLAB prompt.
Data sources: (also available as CSV files)
https://coronavirus.data.gov.uk
https://www.ons.gov.uk/peoplepopulationandcommunity/healthandsocialcare/conditionsanddiseases/datasets/coronaviruscovid19infectionsurveydata
https://covid.joinzoe.com/data#levels-over-time
https://www.gov.uk/guidance/the-r-number-in-the-uk#contents
https://www.gov.uk/government/statistics/transport-use-during-the-coronavirus-covid-19-pandemic
https://www.google.com/covid19/mobility/
Peer-reviewed references [1-6] and archival papers [7-14]
- Friston, K.J., et al., Second waves, social distancing, and the spread of COVID-19 across America. Wellcome Open Research, 2020. 5(103): p. 103.
- Friston, K.J., et al., Dynamic causal modelling of COVID-19. Wellcome Open Research, 2020. 5(89): p. 89.
- Friston, K.J., A. Costello, and D. Pillay, ‘Dark matter’, second waves and epidemiological modelling. BMJ Global Health, 2020. 5(12): p. e003978.
- Gandolfi D, Pagnoni G, Filippini T, et al. Modeling Early Phases of COVID-19 Pandemic in Northern Italy and Its Implication for Outbreak Diffusion. Frontiers in Public Health 2021; 9(1946).
- Friston, K.J., Flandin G., and Razi A. Dynamic causal modelling of COVID-19 and its mitigations. Scientific reports 2022; 12(1): 12419.
- Bowie C, Friston K.J., A twelve-month projection to September 2022 of the Covid-19 epidemic in the UK using a Dynamic Causal Model. Front. Public Health, 2022.
- Moran, R.J., et al., Using the LIST model to Estimate the Effects of Contact Tracing on COVID-19 Endemic Equilibria in England and its Regions. medRxiv, 2020.
- Friston, K.J., G. Flandin, and A. Razi Dynamic causal modelling of mitigated epidemiological outcomes. 2020. arXiv:2011.12400.
- Daunizeau, J., et al., On the reliability of model-based predictions in the context of the current COVID epidemic event: impact of outbreak peak phase and data paucity. medRxiv, 2020.
- Daunizeau, J., et al., Modelling lockdown-induced secondary COVID waves in France. medRxiv, 2020.
- Gandolfi, D., et al., Dynamic causal modeling of the COVID-19 pandemic in northern Italy predicts possible scenarios for the second wave. medRxiv, 2020: p. 2020.08.20.20178798.
- Moran, R.J., et al., Estimating required ‘lockdown’ cycles before immunity to SARS-CoV-2: Model-based analyses of susceptible population sizes, ‘S0’, in seven European countries including the UK and Ireland. medRxiv, 2020: p. 2020.04.10.20060426.
- Friston, K.J., et al., Viral mutation, contact rates and testing: a DCM study of fluctuations. medRxiv, 2021: p. 2021.01.10.21249520.
- Friston, K.J., et al., Tracking and tracing in the UK: a dynamic causal modelling study. arXiv, 2020.
- Report on DCM long-term forecasting - 2nd February 2021
- Report on DCM long-term forecasting - 6th February 2021
- Report on DCM long-term forecasting - 14th February 2021
- Report on DCM long-term forecasting - 21st February 2021
- Report on DCM long-term forecasting - 27th February 2021
- Report on DCM long-term forecasting - 7th March 2021
- Report on DCM long-term forecasting - 14th March 2021
- Report on DCM long-term forecasting - 20th March 2021
- Report on DCM long-term forecasting - 27th March 2021
- Report on DCM long-term forecasting - 4th April 2021
- Report on DCM long-term forecasting - 11th April 2021
- Report on DCM long-term forecasting - 18th April 2021
- Report on DCM long-term forecasting - 24th April 2021
- Report on DCM long-term forecasting - 4th May 2021
- Report on DCM long-term forecasting - 8th May 2021
- Report on DCM long-term forecasting - 17th May 2021
- Report on DCM long-term forecasting - 22nd May 2021
- Report on DCM long-term forecasting - 1st June 2021
- Report on DCM long-term forecasting - 5th June 2021
- Report on DCM long-term forecasting - 16th June 2021
- Report on DCM long-term forecasting - 28th June 2021
- Report on DCM long-term forecasting - 2nd July 2021
- Report on DCM long-term forecasting - 10th July 2021
- Report on DCM long-term forecasting - 17th July 2021
- Report on DCM long-term forecasting - 25th July 2021
- Report on DCM long-term forecasting - 1st August 2021
- Report on DCM long-term forecasting - 5th August 2021
- Report on DCM long-term forecasting - 14th August 2021
- Report on DCM long-term forecasting - 22nd August 2021
- Report on DCM long-term forecasting - 29th August 2021
- Report on DCM long-term forecasting - 6th September 2021
- Report on DCM long-term forecasting - 12th September 2021
- Report on DCM long-term forecasting - 19th September 2021
- Report on DCM long-term forecasting - 25th September 2021
- Report on DCM long-term forecasting - 4th October 2021
- Report on DCM long-term forecasting - 9th October 2021
- Report on DCM long-term forecasting - 3rd November 2021
- Report on DCM long-term forecasting - 9th November 2021
- Report on DCM long-term forecasting - 14th November 2021
- Report on DCM long-term forecasting - 21st November 2021
- Report on DCM long-term forecasting - 27th November 2021
- Report on DCM long-term forecasting - 3rd December 2021
- Report on DCM long-term forecasting - 12th December 2021
- Report on DCM long-term forecasting - 18th December 2021
- Report on DCM long-term forecasting - 30th December 2021
- Report on DCM long-term forecasting - 6th January 2022
- Report on DCM long-term forecasting - 11th January 2022
- Report on DCM long-term forecasting - 17th January 2022
- Report on DCM long-term forecasting - 26th January 2022
- Report on DCM long-term forecasting - 13th February 2022
- Report on DCM long-term forecasting - 19th February 2022
- Report on DCM long-term forecasting - 26th February 2022
- Report on DCM long-term forecasting - 5th March 2022
- Report on DCM long-term forecasting - 12th March 2022
- Report on DCM long-term forecasting - 26th March 2022
- Report on DCM long-term forecasting - 2nd April 2022
- Report on DCM long-term forecasting - 18th April 2022
- Report on DCM long-term forecasting - 18th May 2022
- Report on DCM long-term forecasting - 4th June 2022
- Report on DCM long-term forecasting - 24th July 2022
- Report on DCM long-term forecasting - 27th August 2022
- Report on DCM long-term forecasting - 17th September 2022
- Report on DCM long-term forecasting - 1st October 2022
- Report on DCM long-term forecasting - 17th October 2022
- Report on DCM long-term forecasting - 31st October 2022
- Report on DCM long-term forecasting - 21st November 2022
- Report on DCM long-term forecasting - 4th December 2022
- Report on DCM long-term forecasting - 18th December 2022
- Report on DCM long-term forecasting - 31st December 2022
- Report on DCM long-term forecasting - 8th January 2023
- Report on DCM long-term forecasting - 28th January 2023
- Report on DCM long-term forecasting - 11th February 2023
- Report on DCM long-term forecasting - 25th February 2023
- Report on DCM long-term forecasting - 11th March 2023
- Report on DCM long-term forecasting - 25th March 2023
- Report on DCM long-term forecasting - 7th April 2023
- Report on DCM long-term forecasting - 29th April 2023
- Report on DCM long-term forecasting - 13th May 2023
- Report on DCM long-term forecasting - 27th May 2023
- Report on DCM long-term forecasting - 10th June 2023
- Report on DCM long-term forecasting - 4th July 2023
- Report on DCM long-term forecasting - 23rd July 2023
- Report on DCM long-term forecasting - 26th September 2023
- Report on DCM long-term forecasting - 21st October 2023
- Report on DCM long-term forecasting - 11th November 2023