Skip to content

Bayesian analysis

Specification

Press the Specify 1st-level button. This will call up an fMRI specification job in the batch editor window. Then

  • Load the categorical_spec.mat job file created for the classical analysis.

  • Open Subject/Session, highlight Scans.

  • Deselect the smoothed functional images using the unselect all option available from a right mouse click in the SPM file selector (bottom window).

  • Select the unsmoothed functional images using the ^wa.* filter and select all option available from a right mouse click in the SPM file selector (top right window). The Bayesian analysis uses a spatial prior where the spatial regularity in the signal is estimated from the data. It is therefore not necessary to create smoothed images if you are only going to do a Bayesian analysis.

  • Press Done.

  • Highlight Directory and select the DIR/bayesian directory you created earlier (you will first need to deselect the DIR/categorical directory).

  • Save the job as specify_bayesian.mat and press the Run button.

Estimation

Press the Estimate button. This will call up the specification of an fMRI estimation job in the batch editor window. Then

  • Highlight the Select SPM.mat option and then choose the SPM.mat file saved in the DIR/bayesian subdirectory

  • Highlight Method and select the Choose Bayesian 1st-level option.

  • Save the job as estimate_bayesian.job and press the Run button.

Bayesian analysis: Estimated AR(1) coefficient image indicating heterogeneity near the circle of Willis

SPM will write a number of files into the output directory including

  • An SPM.mat file.

  • Images Cbeta_k.nii where \(k\) indexes the \(k\)th estimated regression coefficient. These filenames are prefixed with a “C”’ indicating that these are the mean values of the “Conditional” or “Posterior” density.

  • Images of error bars/standard deviations on the regression coefficients SDbeta_k.nii.

  • An image of the standard deviation of the error Sess1_SDerror.nii.

  • An image mask.nii indicating which voxels were included in the analysis.

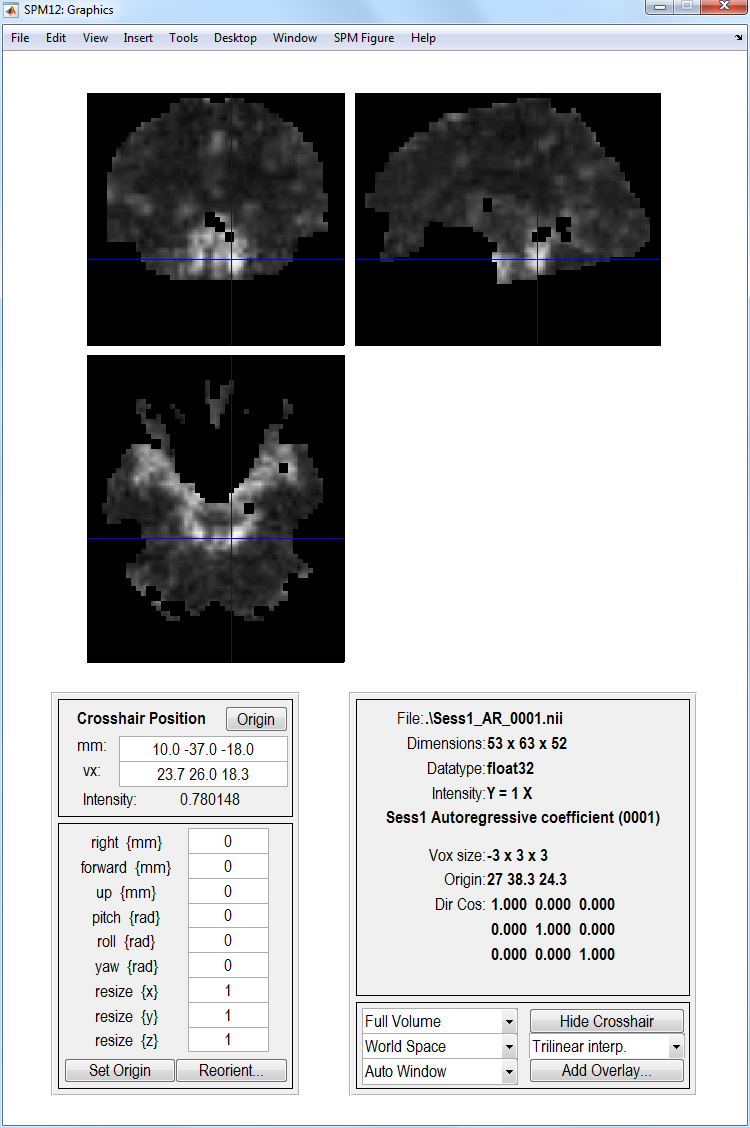
  • Images Sess1_AR_p.nii where \(p\) indexes the \(p\)th AR coefficient. See eg. figure above.

  • Images con_i.nii and con_sd_i.nii which are the mean and standard deviation of the \(i\)th pre-defined contrast.

Inference

After estimation, we can make a posterior inference using a PPM. Basically, we identify regions in which we have a high probability (level of confidence) that the response exceeds a particular size (eg, % signal change). This is quite different from the classical inferences above, where we look for low probabilities of the null hypothesis that the size of the response is zero.

To determine a particular response size (“size threshold”) in units of PEAK % signal change, we first need to do a bit of calculation concerning the scaling of the parameter estimates. The parameter estimates themselves have arbitrary scaling, since they depend on the scaling of the regressors. The scaling of the regressors in the present examples depends on the scaling of the basis functions. To determine this scaling, load the SPM.mat file and type in MATLAB sf = max(SPM.xBF.bf(:,1))/SPM.xBF.dt (alternatively, press Design:Explore:Session 1 and select any of the conditions, then read off the peak height of the canonical HRF basis function (bottom left)).

Then, if you want a size threshold of 1% peak signal change, the value you need to enter for the PPM threshold (ie the number in the units of the parameter estimates) is 1/sf (which should be 4.75 in the present case).1

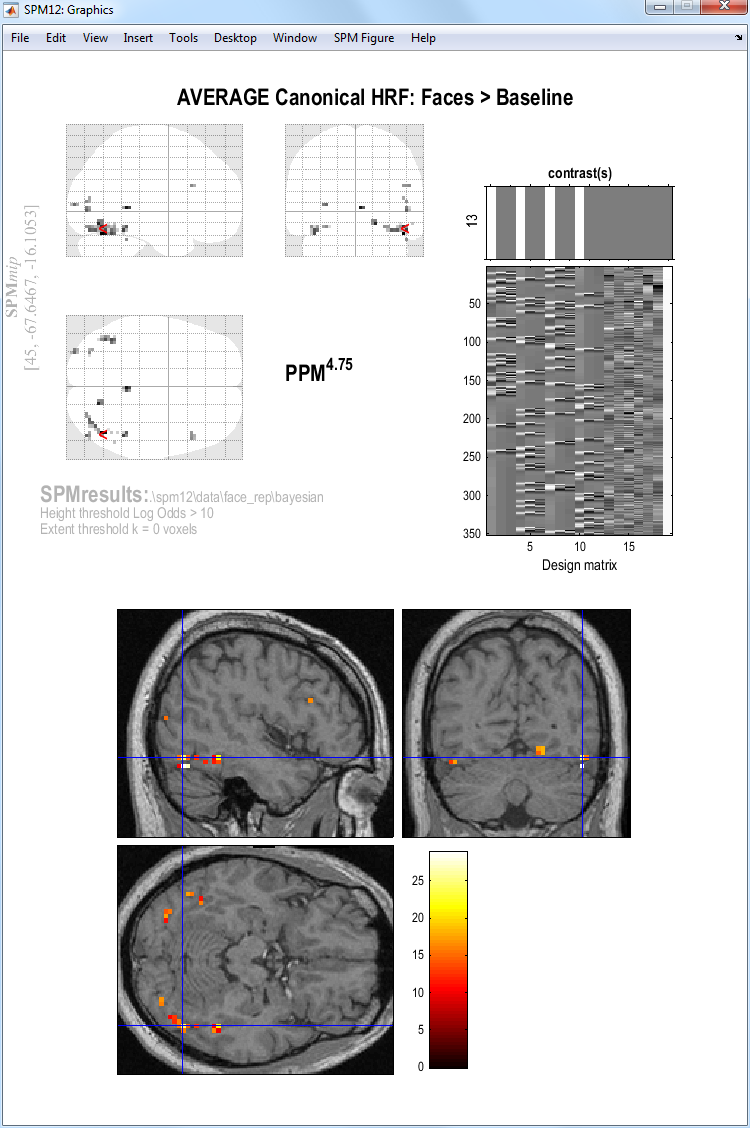
Finally, if we want to ask where is there a signal greater than 1% (with a certain confidence) to faces versus baseline, we need to create a new contrast that takes the AVERAGE of the parameter estimates for the canonical HRF across the four conditions (N1 to F2), rather than the default Positive effect of condition_1 contrast, which actually calculates the SUM of the parameter estimates for the canonical HRF across conditions (the average vs sum makes no difference for the classical statistics).

  • Press Results.

  • Select the SPM.mat file created in the last section.

  • Press Define new contrast, enter the name AVERAGE Canonical HRF: Faces $>$ Baseline, press the T-contrast radio button, enter the contrast [1 0 0 1 0 0 1 0 0 1 0 0]/4, press submit, OK and Done.

  • Apply masking ? [None/Contrast/Image]

    • Specify None.

  • Effect size threshold for PPM

    • Enter the value

  • Log Odds Threshold for PPM

    • Enter the value 10.

  • Extent threshold [0]

    • Accept the default value.

SPM will then plot a map of effect sizes at voxels where it is 95% sure that the effect size is greater than 1% of the global mean. Then use overlays, sections, select the normalised structural image created earlier and move the cursor to the activation in the left hemisphere. This should create the plot below.

Bayesian analysis: MIP and overlay of effect sizes at voxels where PPM is 95% sure that the effect size is greater than 1% of the global mean. The cursor is at the location x=30, y=-82, z=-17 mm

  1. Strictly speaking, this is the peak height of the canonical component of the best fitting BOLD impulse response: the peak of the complete fit would need to take into account all three basis functions and their parameter estimates. ↩