Skip to content

Modelling parametric responses

Parametric modulators

Before setting up the design matrix, we must first load into MATLAB the Stimulus Onsets Times (SOTs), as before, and also the “Lags”, which are specific to this experiment, and which will be used as parametric modulators. The Lags code, for each second presentation of a face (N2 and F2), the number of other faces intervening between this (repeated) presentation and its previous (first) presentation. Both SOTs and Lags are represented by MATLAB cell arrays, stored in the sots.mat file.

  • At the MATLAB command prompt type load sots. This loads the stimulus onset times and the lags (the latter in a cell array called itemlag.

Model specification

Now press the Specify 1st-level button. This will call up the specification of a fMRI specification job in the batch editor window. Then:

  • Press File and Load batch, select the categorical_spec.mat job file you created earlier.

  • Open Conditions and then open the second Condition.

  • Highlight Parametric Modulations, select New Parameter.

  • Highlight Name and enter Lag, highlight values and enter itemlag{2}, highlight polynomial expansion and 2nd order.

  • Now open the fourth Condition under Conditions.

  • Highlight Parametric Modulations, select New Parameter.

  • Highlight Name and enter Lag, highlight values and enter itemlag{4}, highlight polynomial expansion and 2nd order.

  • Open Canonical HRF under Basis Functions, highlight Model derivatives and select No derivatives (to make the design matrix a bit simpler for present purposes!).

  • Highlight Directory and select DIR/parametric (having “unselected” the current definition of directory from the Categorical analysis).

  • Save the job as parametric_spec and press the Run button.

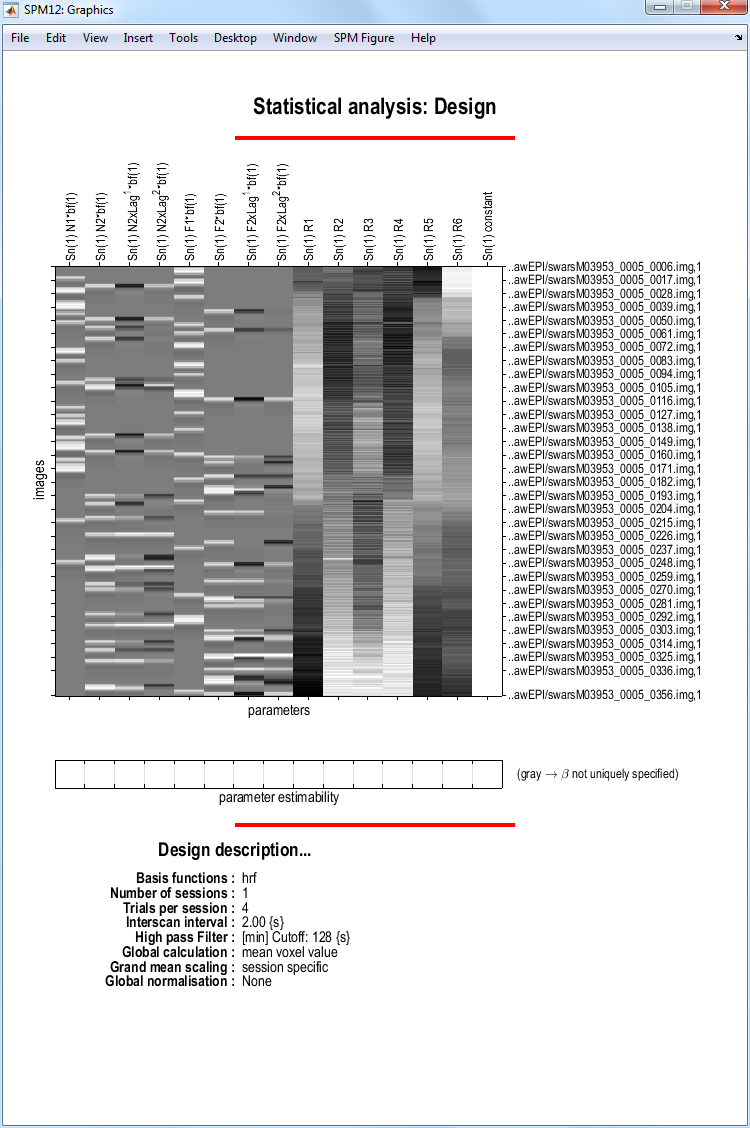
This should produce the design matrix shown below.

Design matrix for testing repetition effects parametrically. Regressor 2 indicates the second occurrence of a nonfamous face. Regressor 3 modulates this linearly as a function of lag (ie. how many faces have been shown since that face was first presented), and regressor 4 modulates this quadratically as a function of lag. Regressors 6,7 and 8 play the same roles, but for famous faces.

Model estimation

Press the Estimate button. This will call up the specification of an fMRI estimation job in the batch editor window. Then

  • Highlight the Select SPM.mat option and then choose the SPM.mat file saved in the DIR/parametric directory.

  • Save the job as parametric_est.job and press the Run button.

SPM will write a number of files into the selected directory including an SPM.mat file.

Plotting parametric responses

We will look at the effect of lag (up to second order, ie using linear and quadratic terms) on the response to repeated Famous faces, within those regions generally activated by faces versus baseline. To do this

  • Press Results and select the SPM.mat file in the DIR/parametric directory.

  • Press Define new contrast, enter the name Famous Lag, press the F-contrast radio button, enter 1:6 9:15 in the columns in reduced design window, press submit, OK and Done.

  • Select the Famous Lag contrast.

  • Apply masking ? [None/Contrast/Image]

    • Specify Contrast.

  • Select the Positive Effect of Condition 1 T contrast.

    • Change to an 0.05 uncorrected mask p-value.

  • Nature of Mask ? inclusive.

  • p value adjustment to control: [FWE/none]

    • Select None.

  • Threshold {F or p value}

    • Accept the default value, 0.001.

  • Extent threshold {voxels} [0]

    • Accept the default value, 0.

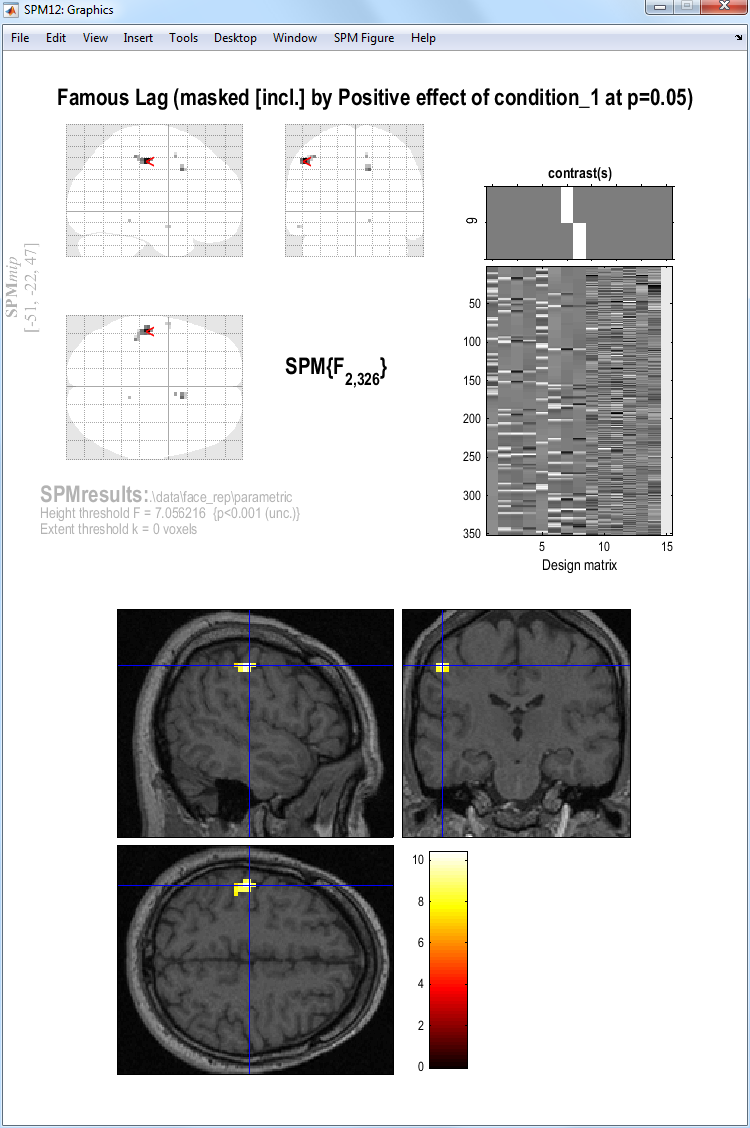
The figure below shows the MIP and an overlay of this parametric effect using overlays, sections and selecting the wmsM03953_0007.nii image.

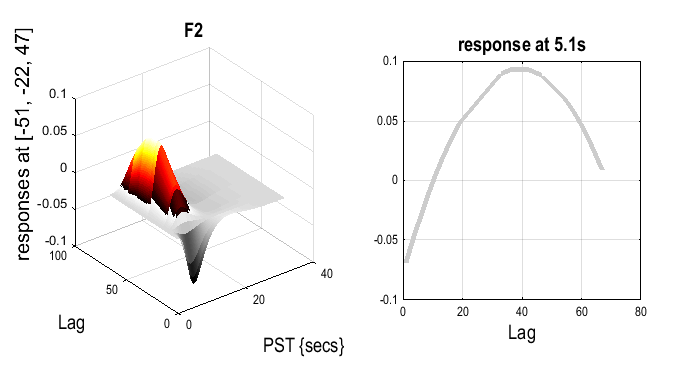
MIP and overlay of parametric lag effect in parietal cortex.

To plot the effect in the time domain:

  • Right clicking on the MIP and selecting global maxima.

  • Pressing Plot, and selecting parametric responses from the pull-down menu.

  • Which effect ? select F2.

This shows a quadratic effect of lag, in which the response appears negative for short-lags, but positive and maximal for lags of about 40 intervening faces (note that this is a very approximate fit, since there are not many trials, and is also confounded by time during the session, since longer lags necessarily occur later (for further discussion of this issue, see the SPM2 example analysis of these data on the webpage).

Response as a function of lag.