Skip to content

Modelling categorical responses

Onset times

Before setting up the design matrix we must first load the Stimulus Onsets Times (SOTs) into MATLAB . SOTs are stored in the sots.mat file in a cell array such that eg. sot{1} contains stimulus onset times in TRs for event type 1, which is N1. Event-types 2, 3 and 4 are N2, F1 and F2.1

  • At the MATLAB command prompt type load sots

Model specification

Now press the Specify 1st-level button. This will call up the specification of a fMRI specification job in the batch editor window. Then

  • For Directory, select the categorical folder you created earlier,

  • In the Timing parameters option,

  • Highlight Units for design and select Scans,

  • Highlight Interscan interval and enter 2,

  • Highlight Microtime resolution and enter 24,

  • Highlight Microtime onset and enter 12. These last two options make the creating of regressors commensurate with the slice-time correction we have applied to the data, given that there are 24 slices and that the reference slice to which the data were slice-time corrected was the 12th (middle slice in time).

  • Highlight Data and Design and select New Subject/Session.

  • Highlight Scans and use SPM’s file selector to choose the 351 smoothed, normalised, slice-time corrected, realigned functional images ie swarsM.img. These can be selected easily using the ^swar.* filter, and select all. Then press Done.

  • Highlight Conditions and select New condition2.

  • Open the newly created Condition option. Highlight Name and enter N1. Highlight Onsets and enter sot{1}. Highlight Durations and enter 0.

  • Highlight Conditions and select Replicate condition.

  • Open the newly created Condition option (the lowest one). Highlight Name and change to N2. Highlight Onsets and enter sot{2}.

  • Highlight Conditions and select Replicate condition.

  • Open the newly created Condition option (the lowest one). Highlight Name and change to F1. Highlight Onsets and enter sot{3}.

  • Highlight Conditions and select Replicate condition.

  • Open the newly created Condition option (the lowest one). Highlight Name and change to F2. Highlight Onsets and enter sot{4}.

  • Highlight Multiple Regressors and select the realignment parameter file rp_sM03953_0005_0006.txt file that was saved during the realignment preprocessing step in the folder containing the fMRI data3.

  • Highlight Factorial Design, select New Factor, open the newly created Factor option, highlight Name and enter Fam, highlight Levels and enter 2.

  • Highlight Factorial Design, select New Factor, open the newly created Factor option, highlight Name and enter Rep, highlight Levels and enter 24.

  • Open Canonical HRF under Basis Functions. Select Model derivatives and select Time and Dispersion derivatives.

  • Highlight Directory and select the DIR/categorical directory you created earlier.

  • Save the job as categorical_spec.mat and press the Run button.

SPM will then write an SPM.mat file to the DIR/categorical directory. It will also plot the design matrix, as shown below

Design matrix

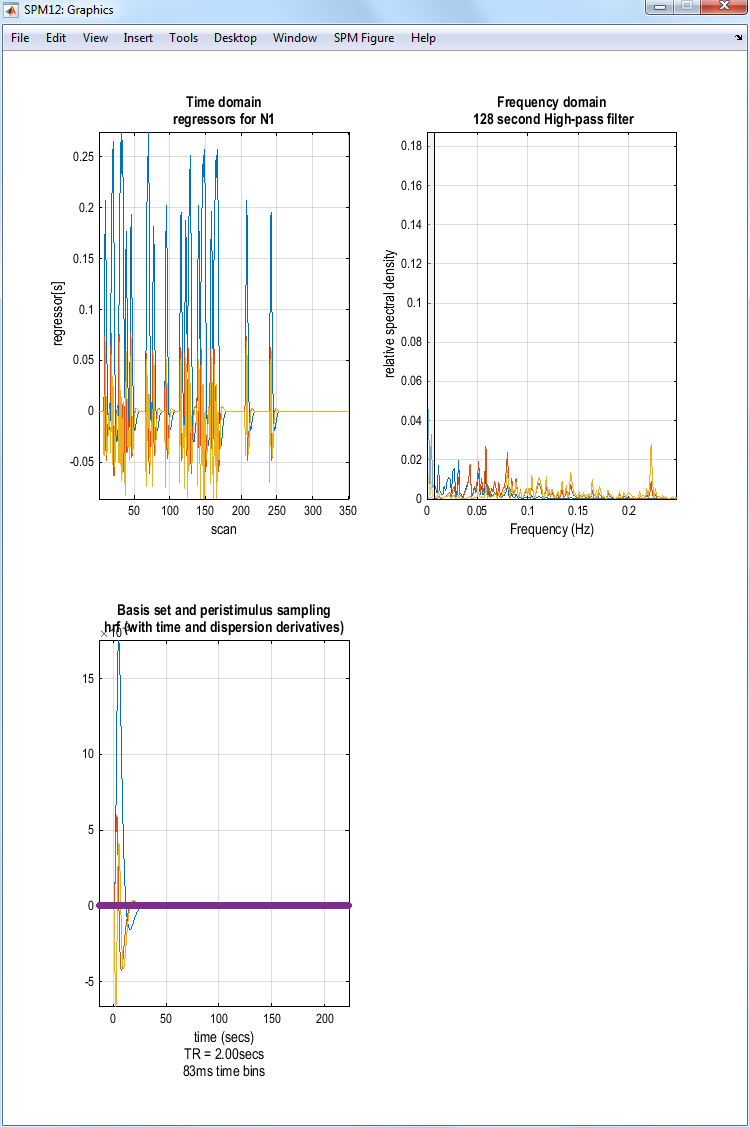
At this stage it is advisable to check your model specification using SPM’s review facility which is accessed via the Review button. This brings up a Design tab on the interactive window clicking on which produces a pulldown menu. If you select the first item Design Matrix SPM will produce the image shown above. If you select Explore then Session 1 then N1, SPM will produce the plots shown below.

Exploring the design matrix. This shows the time series of the "N1" regressor (top left), the three basis functions used to convert assumed neuronal activity into hemodynamic activity (bottom left), and a frequency domain plot of the three regressors for the basis functions in this condition (top right). The frequency domain plot shows that the frequency content of the "N1" condition is generally above the set frequencies that are removed by the High Pass Filter (HPF) (these are shown in grey - in this model we accepted the default HPF cut-off of 128s or 0.008Hz).

Model estimation

Press the Estimate button. This will call up the specification of an fMRI estimation job in the batch editor window. Then

  • Highlight the Select SPM.mat option and then choose the SPM.mat file saved in the DIR/categorical directory.

  • Save the job as categorical_est.job and press Run button.

SPM will write a number of files into the selected directory including an SPM.mat file.

Inference for categorical design

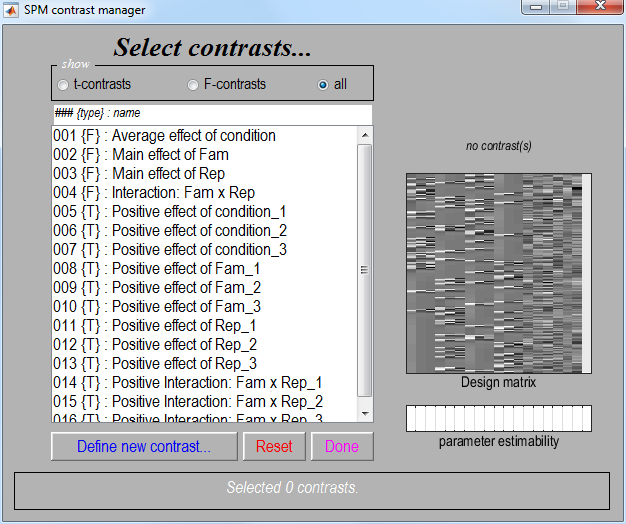
Press “Results” and select the SPM.mat file from DIR/categorical. This will again invoke the contrast manager. Because we specified that our model was using a “Factorial design” a number of contrasts have been specified automatically, as shown below.

Contrast Manager containing default contrasts for categorical design.

  • Select contrast number 5. This is a t-contrast Positive effect of condition_1 This will show regions where the average effect of presenting faces is significantly positive, as modelled by the first regressor (hence the _1), the canonical HRF. Press Done.

  • Apply masking ? [None/Contrast/Image]

    • Specify None.

  • p value adjustment to control: [FWE/none]

    • Select FWE.

  • Corrected p value(family-wise error)

    • Accept the default value, 0.05

  • Extent threshold {voxels} [0]

    • Accept the default value, 0.

SPM will then produce the MIP shown below.

Statistical tables

To get a summary of local maxima, press the whole brain button in the p-values section of the interactive window. This will list all clusters above the chosen level of significance as well as separate (\(>\)8mm apart) maxima within a cluster, with details of significance thresholds and search volume underneath.

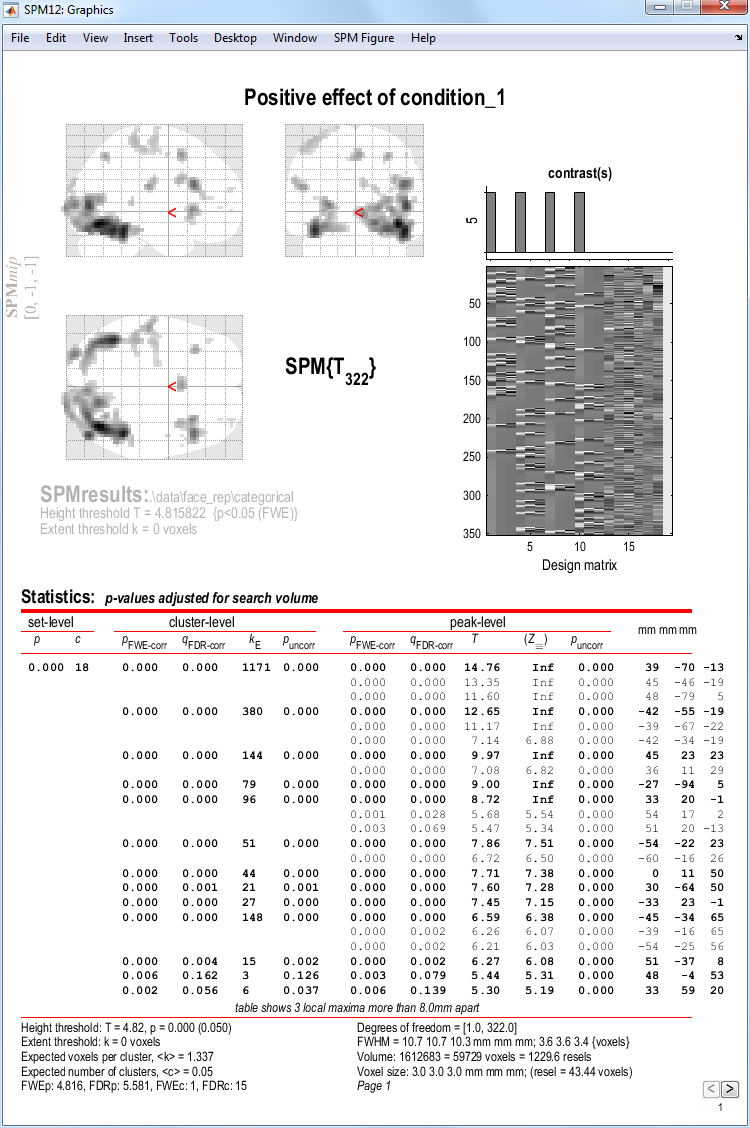
MIP and Volume table for Canonical HRF: Faces > Baseline.

The columns in volume table show, from right to left:

  • x, y, z (mm): coordinates in MNI space for each maximum.

  • peak-level: the chance (p) of finding (under the null hypothesis) a peak with this or a greater height (T- or Z-statistic), corrected (FWE or FDR) / uncorrected for search volume.

  • cluster-level: the chance (p) of finding a cluster with this many(ke) or a greater number of voxels, corrected (FWE or FDR) / uncorrected for search volume.

  • set-level: the chance (p) of finding this (c) or a greater number of clusters in the search volume.

Right-click on the MIP and select goto global maximum. The cursor will move to [39 -70 -14]. You can view this activation on the subject’s normalised, bias-corrected structural (wmsM03953_0007i̇mg), which gives best anatomical precision, or on the normalised mean functional (wmeansM03953_0005_0006.nii), which is closer to the true data and spatial resolution (including distortions in the functional EPI data).

If you select plot and choose Contrast of estimates and 90% C.I (confidence interval), and select the Average effect of condition contrast, you will see three bars corresponding to the parameter estimates for each basis function (summed across the 4 conditions). The BOLD impulse response in this voxel loads mainly on the canonical HRF, but also significantly (given that the error bars do not overlap zero) on the temporal and dispersion derivatives (see next Chapter).

F-contrasts

To assess the main effect of repeating faces, as characterised by both the hrf and its derivatives, an F-contrats is required. This is really asking whether repetition changes the shape of the impulse response (e.g, it might affect its latency but not peak amplitude), at least the range of shapes defined by the three basis functions. Because we have told SPM that we have a factorial design, this required contrast will have been created automatically - it is number 3.

  • Press Results and select the SPM.mat file in the DIR/categorical directory.

  • Select the F-contrast toggle and the contrast number 3, as shown in the next image. Press Done.

  • Apply masking ? [None/Contrast/Image].

    • Specify Contrast.

    • Select contrast 5 - Positive effect of condition_1 (the T-contrast of activation versus baseline, collapsed across conditions, that we evaluated above)

  • uncorrected mask p-value ?

    • Change to 0.001.

  • nature of mask?

    • Select inclusive.

  • p value adjustment to control: [FWE/none]

    • Select none.

  • threshold (F or p value)

    • Accept the default value, 0.001.

  • Extent threshold {voxels} [0]

    • Accept the default value, 0.

A MIP should then appear, the top half of which should look like the figure below.

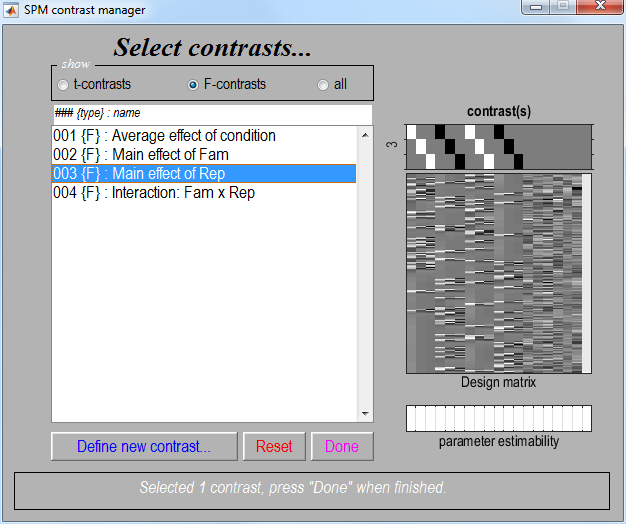
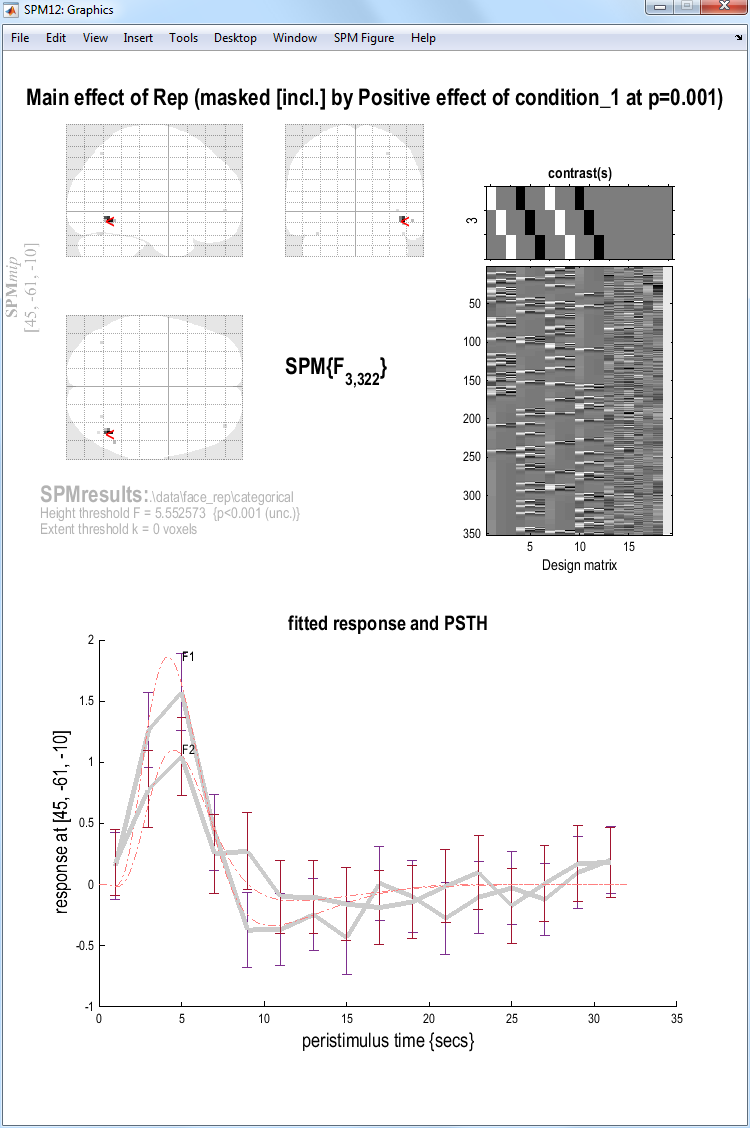
Contrast manager showing selection of the first contrast "Main effect of Rep" (repetition: F1 and N1 vs F2 and N2)
MIP for Main effect of Rep, masked inclusively with Canonical HRF: Faces > Baseline at p<.001 uncorrected. Shown below are the best-fitting responses and peri-stimulus histograms (PSTH) for F1 and F2.

Note that this contrast will identify regions showing any effect of repetition (e.g, decreased or increased amplitudes) within those regions showing activations (on the canonical HRF) to faces versus baseline (at p\(<\).05 uncorrected). Select “goto global max”, which is in right ventral temporal cortex [42 -64 -8].

If you press plot and select Event-related responses, then F1, then fitted response and PSTH, you will see the best fitting linear combination of the canonical HRF and its two derivatives (thin red line), plus the “selectively-averaged” data (peri-stimulus histogram, PSTH), based on an FIR refit (see next Chapter). If you then select the hold button on the Interactive window, and then plot and repeat the above process for the F2 rather than F1 condition, you will see two estimated event-related responses, in which repetition decreases the peak response (ie F2\(<\)F1), as shown in the figure above.

You can explore further F-contrasts, which are a powerful tool once you understand them. For example, the MIP produced by the “Average effect of condition” F-contrast looks similar to the earlier T-contrast, but importantly shows the areas for which the sums across conditions of the parameter estimates for the canonical hrf and/or its temporal derivative and/or its dispersion derivative are different from zero (baseline). The first row of this F-contrast ([1 0 0 1 0 0 1 0 0 1 0 0]) is also a two-tailed version of the above T-contrast, ie testing for both activations and deactivations versus baseline. This also means that the F-contrasts [1 0 0 1 0 0 1 0 0 1 0 0] and [-1 0 0 -1 0 0 -1 0 0 -1 0 0] are equivalent. Finally, note that an F- (or t-) contrast such as [1 1 1 1 1 1 1 1 1 1 1], which tests whether the mean of the canonical hrf AND its derivatives for all conditions are different from (larger than) zero is not sensible. This is because the canonical hrf and its temporal derivative may cancel each other out while being significant in their own right. The basis functions are really quite different things, and need to represent separate rows in an F-contrast.

F-contrasts for testing effects of movement

To assess movement-related activation

  • Press Results, select the SPM.mat file, select F-contrast in the Contrast Manager. Specify e.g. Movement-related effects (name) and in the contrasts weights matrix window, or 1:12 19 in the columns for reduced design window.

  • Submit and select the contrast, specify Apply masking? (none), corrected height threshold (FWE), and corrected p-value (accept default).

  • When the MIP appears, select sections from the overlays pulldown menu, and select the normalised structural image (wmsM03953_0007.nii).

You will see there is a lot of residual movement-related artifact in the data (despite spatial realignment), which tends to be concentrated near the boundaries of tissue types (eg the edge of the brain; see below). (Note how the MIP can be misleading in this respect, since though it appears that the whole brain is affected, this reflects the nature of the (X-ray like) projections onto each orthogonal view; displaying the same data as sections in 3D shows that not every voxel is suprathreshold.) Even though we are not interested in such artifact, by including the realignment parameters in our design matrix, we “covary out” (linear components) of subject movement, reducing the residual error, and hence improve our statistics for the effects of interest.

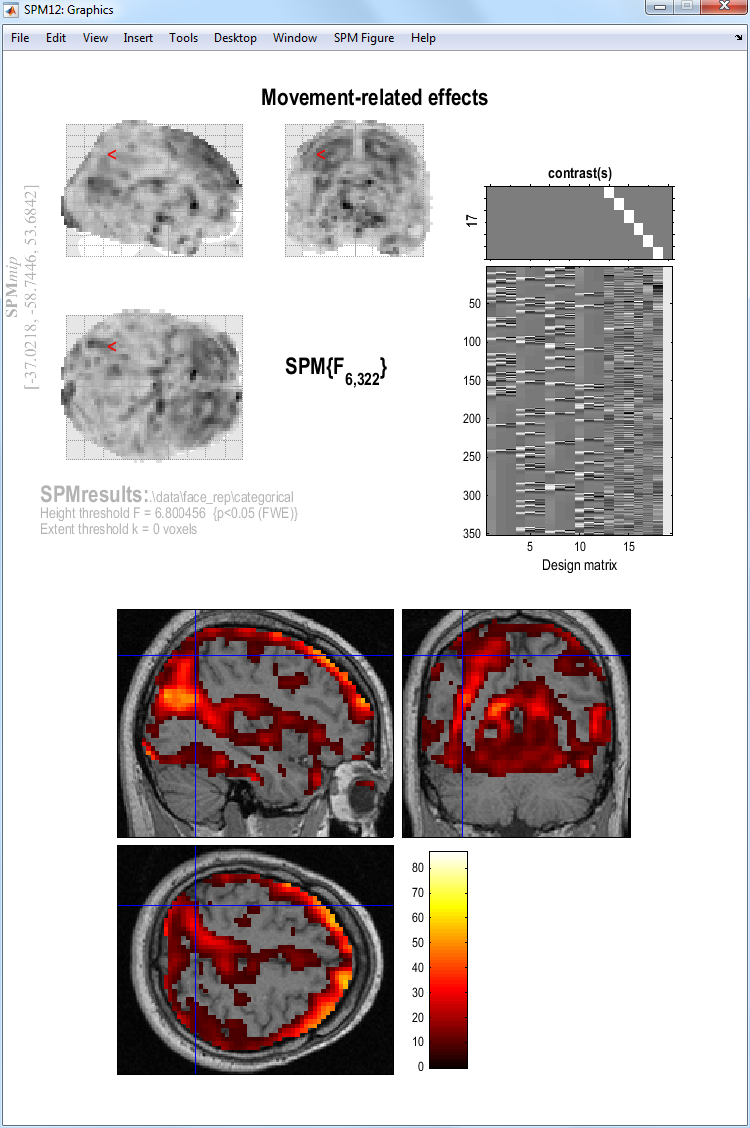
Movement-related activations. These spurious ‘activations’ are due to residual movement of the head during scanning. These effects occur at tissue boundaries and boundaries between brain and non-brain, as this is where contrast differences are greatest. Including these regressors in the design matrix means these effects cannot be falsely attributed to neuronal activity.

  1. Unlike previous analyses of these data in SPM99 and SPM2, we will not bother with extra event-types for the (rare) error trials. ↩

  2. It is also possible to enter information about all of the conditions in one go. This requires much less button pressing and can be implemented by highlighting the “Multiple conditions” option and then selecting the all-conditions.mat file, which is also provided on the webpage. ↩

  3. It is also possible to enter regressors one by one by highlighting “Regressors” and selecting “New Regressor” for each one. Here, we benefit from the fact that the realignment stage produced a text file with the correct number of rows (351) and columns (6) for SPM to add 6 regressors to model (linear) rigid-body movement effects. ↩

  4. The order of naming these factors is important - the factor to be specified first is the one that “changes slowest” ie. as we go through the list of conditions N1, N2, F1, F2 the factor “repetition” changes every condition and the factor “fame” changes every other condition. So “Fam” changes slowest and is entered first. ↩